How Do Fractals Appear in Nature and Mathematics

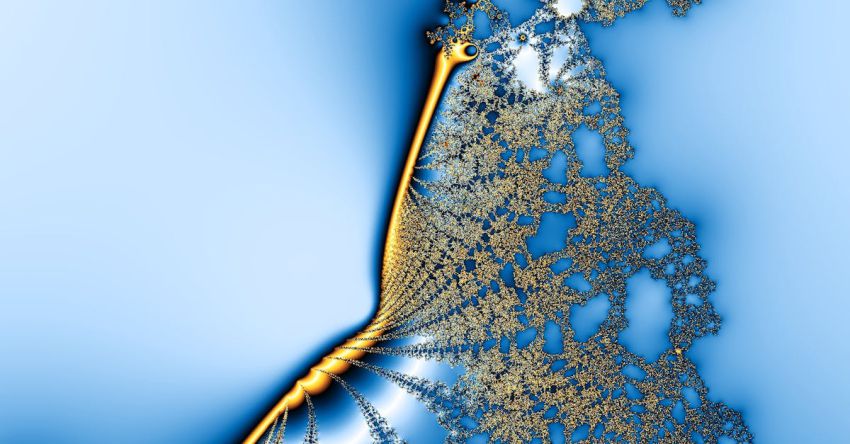
Fractals, the intricate and mesmerizing patterns found in both nature and mathematics, have captivated the curiosity of scientists, mathematicians, and artists alike. These self-replicating geometric shapes are characterized by their infinite complexity and self-similarity at different scales. From the intricate branches of a tree to the intricate structure of a snowflake, fractals can be observed in various forms in the natural world. Moreover, they play a crucial role in various mathematical theories and applications, making them a fascinating subject of study that bridges the gap between art, science, and mathematics.

Fractals in Nature:

Nature is a treasure trove of fractal patterns, with examples found in various phenomena ranging from the branching patterns of trees to the intricate shapes of coastlines and clouds. One of the most famous examples of fractals in nature is the Romanesco broccoli, a vegetable that exhibits a natural fractal pattern in the form of a cone composed of smaller conical shapes, each a replica of the whole. Similarly, the branching patterns of trees and rivers exhibit self-similarity, where the smaller branches or tributaries mirror the overall structure of the larger tree or river.

Another striking example of fractals in nature is the coastline paradox, which states that the length of a coastline becomes infinitely long as the measuring scale becomes smaller. This phenomenon is a classic example of self-similarity in nature, where the intricate details of a coastline repeat themselves at different scales, creating a fractal pattern that is both beautiful and infinitely complex.

Fractals in Mathematics:

In mathematics, fractals are defined as geometric shapes that exhibit self-similarity at different scales, meaning that they look the same or similar regardless of the magnification level. The Mandelbrot set, discovered by mathematician Benoit B. Mandelbrot in the 1980s, is one of the most famous examples of a fractal in mathematics. The Mandelbrot set is a complex set of points in the complex plane that, when iterated through a simple mathematical formula, create intricate and infinitely detailed patterns that exhibit self-similarity at different scales.

Fractal geometry, a branch of mathematics that deals with the study of fractals, has found applications in various fields such as computer graphics, image compression, and chaos theory. Fractal patterns are also used in the creation of realistic landscapes in computer-generated imagery and the modeling of natural phenomena such as clouds and mountains. The mathematical beauty and complexity of fractals have inspired artists, mathematicians, and scientists to explore their properties and applications in different fields.

The Beauty of Fractals:

The allure of fractals lies in their infinite complexity and beauty, which can be observed in the natural world and recreated through mathematical formulas and computer algorithms. The intricate patterns of fractals evoke a sense of wonder and awe, captivating the imagination and inspiring creativity in those who study them. Whether in the delicate structure of a snowflake or the branching patterns of a tree, fractals remind us of the interconnectedness and beauty of the natural world.

Fractals are not just mathematical curiosities or artistic inspirations; they are a fundamental part of the fabric of the universe, shaping the way we perceive and understand the world around us. The study of fractals bridges the gap between art, science, and mathematics, offering a glimpse into the underlying patterns and structures that govern the complexity of nature. The beauty of fractals lies in their ability to capture the essence of the natural world in all its intricate and infinitely detailed glory.